分散とは、ばらつきを表す指標です。
分散と名前がつく統計用語に、標本分散と不偏分散があります。
本記事では、それぞれの用語の意味合いを明確にし、求め方まで解説します。
標本と母集団の分散
母集団について知りたい場合、母集団の一部である標本を抽出して推測します。
標本を知ることで母集団がわかるという理論であるため、標本の分散=母集団の分散と考えてしまいますが、
厳密には異なります。
そのため、母集団の分散を母分散、標本の分散を標本分散とし、分けて考えるのです。
不偏分散とは
不偏分散とは、母分散を推定するための分散です。
標本分散=母分散ではないため、母分散を求める場合は標本分散をアレンジして母分散を推定します。
母分散を推定するために標本分散をアレンジして求めた分散こそが、不偏分散です。
標本分散の求め方
標本分散は、偏差(観測値ー平均値)の二乗の和を、データ数で割ることで求められます。
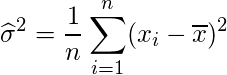
不偏分散の求め方
不偏分散は、データ数−1で割ります。
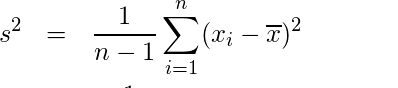
不偏とは、言葉の通り「偏りがない」という意味です。
n-1で割ることで、母集団に対する標本の偏りを緩和します。
なぜn-1で割ると、不偏分散になるの?
標本は母集団に比べると、データが偏る傾向にあるため、標本分散は母分散より小さな値になりがりなんだ。
そこで、n-1で割ることで、少しだけ補正しているよ。
※なぜ1で引く必要があるのかは別記事を御覧ください。
不偏分散の標準偏差
分散の平方根は標準偏差だから、不偏分散の平方根は、母集団の標準偏差を推定できる不変標準偏差ってこと?
そう考えがちだけど、違うよ
「不偏」がつく統計用語は、母集団の性質の不偏推定量といえます。
ですが、不偏分散の平方根は、不偏標準偏差の不偏推定量ではないので注意しましょう。
不変標準偏差は、不偏分散の平方根を補正した値になります。
不偏分散を出す段階で、n-1で割っているから補正が完了していると思っていたけど、
不偏標準偏差を出す場合は平方根を出してから、更に補正する必要があるんだね。











