質的変数と量的変数は、測定尺度の観点で分類することができます。
本記事を読むと、次のことがわかります。
・名義尺度、順序尺度、間隔尺度、比例尺度の4尺度の違いがわかる
測定尺度とは
測定尺度とは、データを値が持つ性質ごとに整理する基準のことです。
よくわからない…
質的変数・量的変数を、さらにカテゴライズするときの基準だと思えば、大丈夫!
質的変数や量的変数の意味については、こちらの記事をご参照ください。
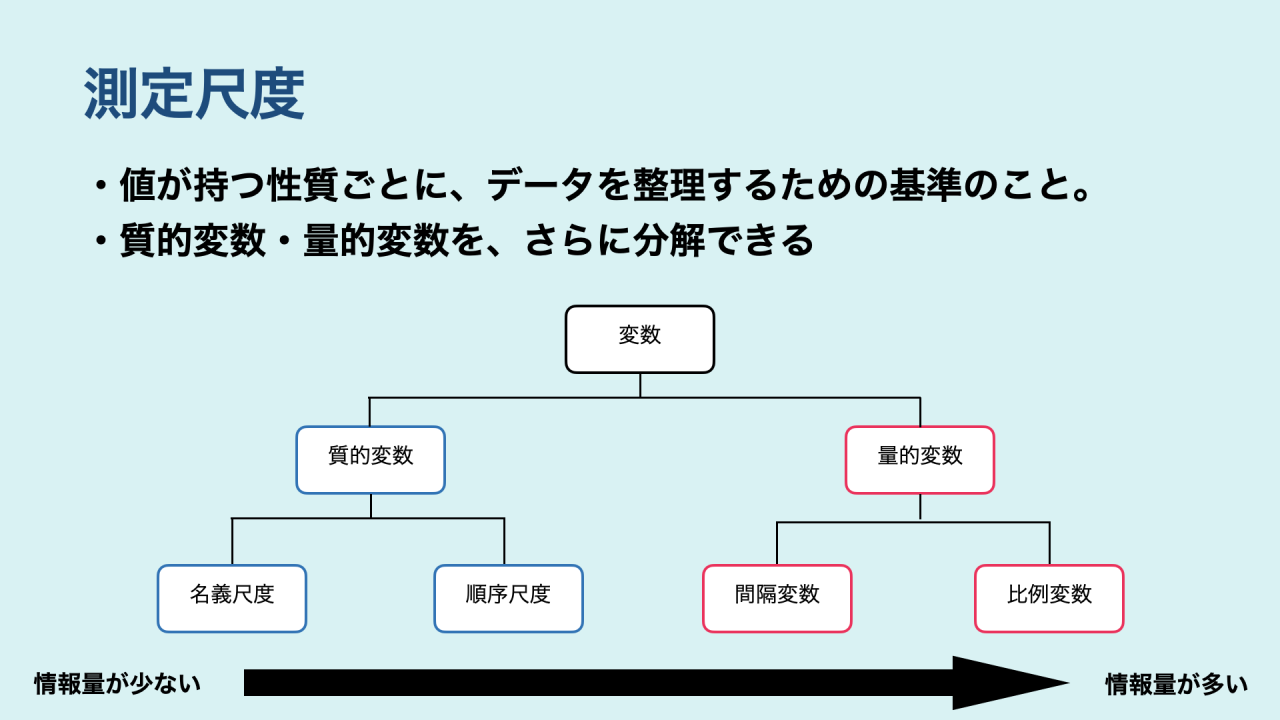
測定尺度は、名義尺度・順序尺度・比例尺度・間隔尺度の4種類です。
質的変数は名義尺度と順序尺度に分けられ、量的変数は比例尺度と間隔尺度に分けられます。
図で表すと、下記のイメージです。
名義尺度
同じ値かどうかを判断するためのデータです。
質的変数に用いられる尺度です。
例えば、下記のようなデータは名義尺度です。
- 花の種類
- 名前
- 性別
- 血液型
- 電話番号
名義尺度には、データ同士に大小が無いのが特徴です。
データの大小って、どういう意味?
「性別」を例にとって説明しましょう。
性別が「男」であるデータと「女」であるデータを比較しても、どちらかが大きい・小さいという評価は出来ないよね。
これは、名義尺度である「性別」というデータには、大小関係がないからなんだ!
順序尺度
順序尺度とは、数字の順番に意味があるものを指します。
順序尺度も、質的変数をカテゴライズするための尺度です。
例えば、下記のデータは順序尺度です。
- 成績の5段階評価
- 徒競走の順位

名義尺度との違いは、データ同士に大小関係があることです。
例えば、徒競走の順位が1位の人と2位の人では、1位の方が「足が速い」と評価できます。
間隔尺度
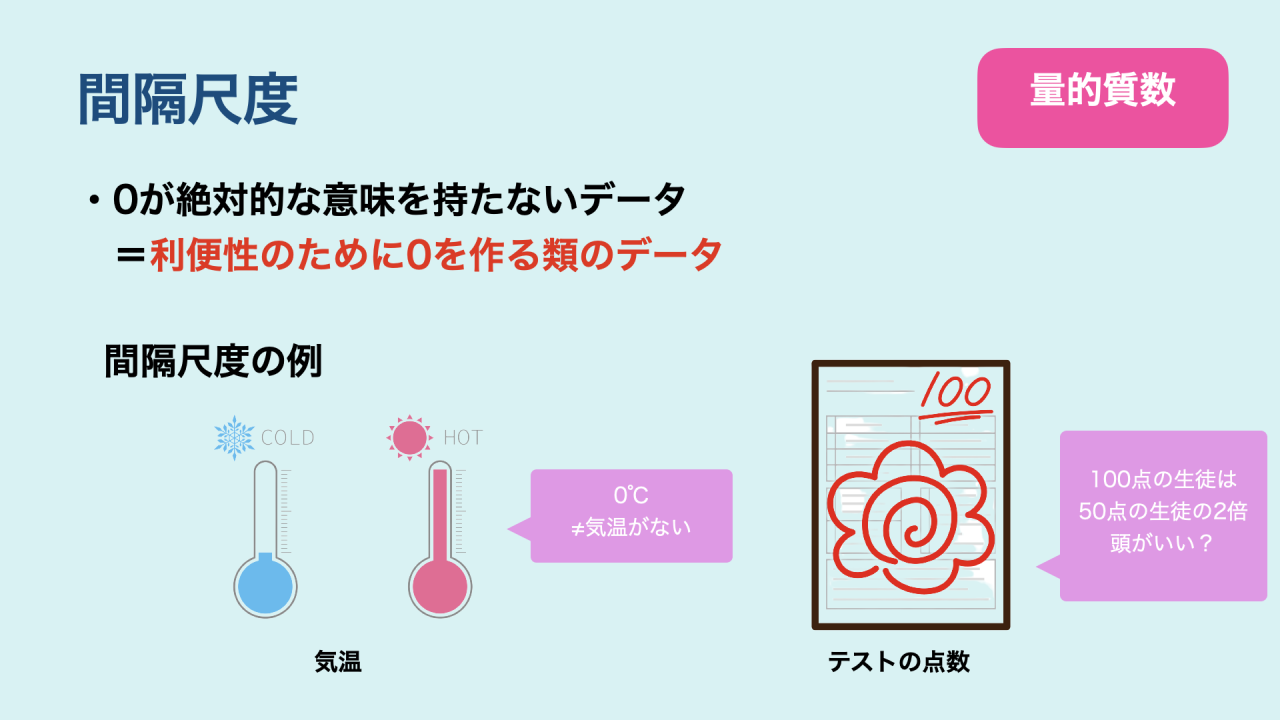
間隔尺度とは、0が絶対的な意味合いを持たないものを指します。
つまり、利便性のために作った0を使うデータのことです。
「0が絶対的な意味を持たない」って、どういう意味?
間隔尺度における0は、「意味を持たない」というわけではなく、単なる目盛りの1種でしかないのです。
例えば、気温が0℃だとしても「気温がない・温度がない」というわけではないですよね。
あくまでも0°Cという目盛りの一つに過ぎないというわけです。
だから、間隔の差分を計る足し算引き算は対応できるけれど、掛け算割り算はできません。
例)「気温が20°Cの日は、10℃の日より2倍暑い」と言えない
確かに、平均気温に比べて、0℃は相対的に寒いとは言えるけど、気温がないということではないよね。
「0℃で水が氷になる」みたいに、0℃で何かの変化がある訳でもないし!
そう!
あくまでも相対的な意味しか持たないんだ!
数量的データを扱うため、量的変数に対して用いられる尺度です。
例えば、下記のデータは間隔尺度に該当します。
- 気温
- テストの点数
- 偏差値
比例尺度
間隔尺度とは異なり、比例尺度は0が絶対的な意味を持ちます。
例えば下記のデータが比例尺度です。
- 距離
- 時間
- 速度
地点Aと地点Bの距離が0mなのであれば、AとBの間には距離がない(同一地点である)と言えるよね。
間隔尺度の0と違って、0に意味があるんだ。
だから、比例尺度は掛け算割り算の計算ができるよ。
例)「1000mは500mの2倍の距離だ」と言える
測定尺度の優劣
測定尺度の中には、順序があります。
名義尺度が最もシンプルで、尺度が上位であるほど変数の持ち合わせる意味が増えます。
名義尺度の特徴に+αされるイメージです。
表でまとめると、下記のようになります。
| 測定尺度 | 特徴 | できること |
| 名義尺度 | ・値が同じか否か | カウントのみ ※最頻値が使われる |
| 順序尺度 | ・値が同じか否か ・大小関係があるか | カウント 中央値が意味を持つ |
| 間隔尺度 | ・値が同じか否か ・大小関係があるか ・データ間の差に意味がある | カウント 中央値が意味を持つ 足し算・引き算 |
| 比例尺度 | ・値が同じか否か ・大小関係があるか ・データ間の差に意味がある ・0が絶対的な意味を持つ | カウント 中央値が意味を持つ 足し算・引き算 掛け算・割り算 |
上位の尺度は、下位の尺度の統計量を用いることができます。












