データの前処理とは
データの前処理とは、分析に入る前に収集したデータを分析に使えるよう加工することです。
例えば、「テキストデータを数字表現にする」、「大きさの規模感を統一する」、「分布の偏りを調整する」などの処理を、前処理で行います。
なぜデータの前処理が必要なのか
前処理が必要な理由は、適切なデータ分析を行うためです。
前処理を行わずに、欠陥や不備のあるデータをそのまま分析すると、途中でエラーが起きたり、分析結果にゆがみが生じたりする危険性があります。
また、ゆがんだ分析結果をもとに、ビジネス上の意思決定をしてしまうと、損失や無駄が増えてしまいます。
そういった危険性を排除するため、前処理は行われます。
分析工程としては必要不可欠なフェーズです。
どの段階で行うのか
前処理は、データ分析の前に行います。
「データの前処理は全行程の8割を占める」と言われるほど、非常に多くの時間を費やします。
データ分析を本格的に学びたい方は、プログラミングスクールがおすすめです!
おすすめスクールは、こちらからCHECK!
データの前処理が必要な場面とは?
ここからは、データセットの状態別で、前処理工程の方法を見ていきましょう。
特徴量の種類が多すぎる時(次元削減)
特徴量とは、データの項目のことを指す用語です。
例えば、下記のようなデータセットがあるとします。
この場合の特徴量は、「品物名」「値段」「個数」「売上」「再来店」「交通機関」を指します。
今回のデータセットは、特徴量が6つとなっていますね。
| 品物名 | 値段 | 個数 | 売上 | 再来店 | 交通機関 | |
| Aさん | りんご | 100 | 4 | 400 | 再来店した | 電車 |
| Bさん | ぶどう | 150 | 2 | 300 | 再来店しなかった | 車 |
特徴量を6つも使うと、計算が大変なので、今回は2つに絞りたいです。
このように、扱う項目数を減らすことを次元削減と呼びます。
特徴量を4つ削減する必要があるわけですが、どの特徴量を選べばいいか、パッと見ただけでは、わかりません。
とても重要な特徴量を勝手に使わないことにしてしまうと、精度の低い結果しか出ないことになってしまいます。
このような場合に、PCA(主成分分析)を使うことで、特徴量を選別することができます。
PCA(主成分分析)
PCAは、データの特徴量間の関係性などを分析することで、主成分(求めたい結果への影響力が強い特徴量)を見つけるための手法です。
PCAを使うと、扱う項目数が多い場合に、いくつかの重要な項目を抽出することができます。
PCAについては、Youtubeでも解説しています。
ぜひ御覧ください
単位が異なる特徴量同士を比較したい時
単位が異なる特徴量を比べる時、なぜ前処理が必要なのでしょうか?
例えば、身長1.8mのAさんと体重70kgのBさんがいるとします。
2人のうち、どちらが平均よりも身長(体重)が大きいと言えるのでしょうか?
単純に平均の値からそれぞれのデータ値を引くという方法が取れそうです。
しかし、そもそも身長体重を比較することが難しいですね。
それは、単位(m・kg)が異なるからです。
この場合は、身長・体重それぞれのデータを標準化し、身長・体重の単位を揃えてあげることで、比較しやすくすることができます。
標準化
標準化とは、データをある範囲に納めることで、項目同士のばらつきを減らすための手法です。
標準化を行うと、各データを0~1の範囲の中に納めることができます。
標準化の公式は下記です。
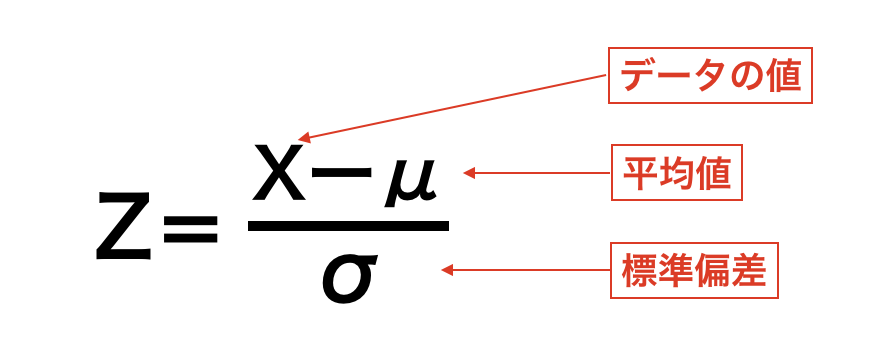
標準化した結果、身長1.8mが0.6、体重70kgが0.8だとわかった場合、体重70kgのBさんの方が平均よりも値が大きかったとわかります。
欠損値がある場合
値が何も入っていない箇所(NaNで表示される箇所)があると、うまく分析できない場合があります。
そのため、分析前に予め欠損値の処理を行う必要があります。
欠損値がある場合は、以下の方法が取られます。
- データの中央値や平均値などで補填する
- 欠損値が多すぎる場合は、その特徴量を使わない
文字列がある時
コンピュータが読み取れるのは数字だけです。
文字列がある場合は、数字への変換が必要になります。
先程の果物屋さんデータベースを例に、考えてみましょう。
| 品物名 | 値段 | 個数 | 売上 | 再来店 | 交通機関 | ||
| Aさん | りんご | 100 | 4 | 400 | 再来店した | 電車 | |
| Bさん | ぶどう | 150 | 2 | 300 | 再来店しなかった | 車 |
品物名・再来店・交通機関が文字になっていますね。
この内、再来店は「する」・「しない」の二択になっていることがわかります。
よって、再来店する場合を0、再来店しない場合を1にすることで、数字化することができます。
品物名・交通機関のように、選択肢が2つよりも多い場合の変換方法は2種類あります。
バイナリーエンコーディング
バイナリーエンコーディングでは、すべての特徴量を2進数で表現することから始めます。
品物名の種類が、「りんご」「バナナ」「ぶどう」の3種類だった場合、下記のような表示に変更されます。
| 2進数 | |
| りんご | 01 |
| バナナ | 10 |
| ぶどう | 11 |
続いて、2進数にした数を2つの変数に入れ込みます。
| 変数1 | 変数2 | (2進数) | |
| りんご | 0 | 1 | 01 |
| バナナ | 1 | 0 | 10 |
| ぶどう | 1 | 1 | 11 |
バイナリーエンコーディングは、種類が多い場合(りんご、ぶどう、、などの種類のこと)でも少ない数で表現できます。
しかし、りんご(01)の数字を入れ替えると、バナナ(10)になるから、「りんごの反対はバナナである」という、お互いの相関が含まれてしまう点がデメリットです。
ワンホットエンコーディング
相関が含まれないように作られたエンコーディングが、「ワンホットエンコーディング」です。
こちらでは、該当するものにだけ、1を与えます。
| りんご(変数1) | バナナ(変数2) | ぶどう(変数3) | |
| りんご | 1 | 0 | 0 |
| バナナ | 0 | 1 | 0 |
| ぶどう | 0 | 0 | 1 |
このように、「りんご」なら「りんご」のみを1とすることで、相関のない変換を行うことができます。
しかし、ワンホットエンコーディングでは非常に多くの変数が必要になります。
バイナリーエンコーディングとワンホットエンコーディングの使い分けとしては、以下のような形で行います。
| ワンホットエンコーディング | バイナリーエンコーディング | |
| 使い分け | 2~3のカテゴリ | たくさんのカテゴリ |
最後に
今回は、前処理に焦点を当ててご説明しました。
データサイエンスをもっと詳しく知りたい方は、Youtubeでも解説しています。
ぜひご活用ください。
データ分析を本格的に学びたい方は、プログラミングスクールがおすすめです!
おすすめスクールは、こちらからCHECK!











